中学校までは数学が得意だったのに、高校になってから苦手になってしまった・・・
そのような悩みを持つ高校生が多いようです。高校数学と中学数学の大きな違いの1つに「文字の扱い」があります。中学数学では方程式をたてるとき、xやyを用いることはありますが、【多くの文字を含む式】の証明問題を解くことはありません。これが高校数学でつまずいてしまう大きな要因ではないでしょうか?
先日読んだ書籍『高校生が感動した数学の物語』がとても参考になり、タイトルにもあるように数学好きなら感動するような内容でしたので、備忘録として記録しておきたいと思います。
私は、高校数学がめちゃめちゃ得意というわけではないので、難関大学合格レベルの指導はちょっと自信がないのですが、この本を読み、高校数学の基本的な考え方を思い出すことができました。高校数学に悩む生徒や中学数学が得意な生徒にこの本から得られた「数学は感動する学問だ」ということを少しでも共感していただけたらと思います。
方程式を解くための大原則

高校数学ではこのような文字を多く含む等式の証明問題をよく見かけます。本書では、この問題を解くために使う知識は中学数学の知識だけ、と書いてありましたが、実際は方程式を解くための大原則を理解していないと解くことは難しいかもしれません。
【等式条件の原則】
- まず文字消去(文字変換)が基本
- 定数の消去に用いる
- 全体消去に用いる
- 次数下げに用いる
このどれかを用いるとなんとか等式を解くことができるようです。(お付き合いいただければと思います)
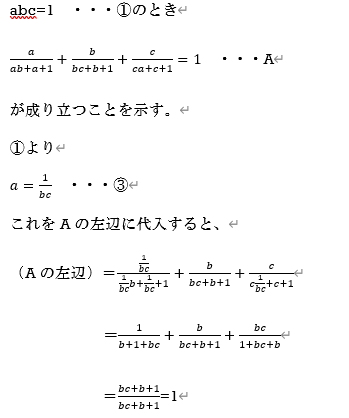
という流れになります。
つまり、条件式③を利用して1文字aを消去するという考え方は、等式条件の基本であっても、ずっと計算していかないと、どのような流れになるかわかりにくいのです。
【式変換の原則】
式変換をするときは嫌なものに対して
- 嫌なものをなくす
- 嫌なものを移項、分離する
- 嫌なものを無視して考える
- 嫌なものを置き換える
- 式の目標は因数分解が基本
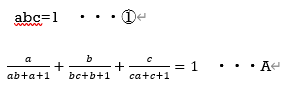
この1つの問題に対して少なくとも4つの解法を本書では解説していました。(今回は他3つの解法は割愛します)
伝説の予備校講師と言われた山本矩一郎先生は、数学を一言で表すと「自由な発想と工夫の宝庫」という表現をしています。また、数学の信条について「論理は後、発見が先」とおっしゃっています。
デカルトに学ぶ、現代を生きるための学問
17世紀フランスの哲学者ルネ・デカルトの有名な言葉「我思う、ゆえに我あり」が本書でも紹介されていました。デカルトは哲学者として有名で、倫理や世界史に登場する人物ですが、実は彼自身は専ら数学者でもあったのです。彼が子どもの頃、通っていた学校はカトリック信仰に基づいた、厳格なキリスト教を教える学校だったようです。しかし、物理や数学に魅了され、その学問を深く探求していくうちに、神学(宗教)の非厳密性に疑問を持つようになります。そして、意志や感覚をすべて数学のように「真」か「偽」で表していくようになります。
- 計算は時々間違えることがあるから、すべてを計算で考えることは「偽」
- 感覚もしばしば間違えることがあるから、感覚で判断することも「偽」
つまり、自分が生きている中で、何が「真」であるかを突き詰めていくことにより、
“たとえ世の中のすべてのことを疑い、自分の存在さえも疑ったとしても、それを見つめている「我」だけは、その存在を疑うことはできない”
と哲学の考えをすすめていき、哲学史上もっとも有名な「我思う、ゆえに我あり」という言葉が現れました。原語では、「私は考えている、それゆえ私は存在している。考えているということがゆえに自分の存在なのだ」という意味です。
基礎学習の積み重ねが自分の心と向き合う練習
現代人はときおり、自分を見失いがちになります。実は私も昔、そんな時期がありました。現代社会の忙しさ、ストレス、悲しい出来事、辛い経験・・・
自分はなんでこうなんだろうと悲観したくなった経験はありませんか?もしくは、周りの環境が自分の思うように行かず、どうしたらよいか悩んだり。そういう時は、ちょっと目の前の問題から離れて自分の心の声を聞いてみてください。
自分がどうしたいのか、どうすればいいのか、少しずつ聞こえてくるかもしれません。
まだ聞こえてこないという方は、「我思う、ゆえに我あり」を考えてみてください。
子どものうちにしっかりと基礎学習を行うことは、数学に限らず、どの分野の学習でも世の中の原理原則を考え、自分自身と向き合う心を育む練習になるかもしれません。

















